一文搞懂什么是粒子群优化算法(Particle Swarm Optimization，PSO)【附应用举例】

代码链接放在文末！

本文参考了很多张军老师《计算智能》的第六章知识。

本文来源：https://blog.csdn.net/qq_44186838/article/details/109181453

粒子群优化算法

1.1 粒子群优化算法简介

粒子群优化算法（Particle Swarm Optimization，PSO）是进化计算的一个分支，是一种模拟自然界的生物活动的随机搜索算法。

PSO模拟了自然界鸟群捕食和鱼群捕食的过程。通过群体中的协作寻找到问题的全局最优解。它是1995年由美国学者Eberhart和Kennedy提出的，现在已经广泛应用于各种工程领域的优化问题之中。

1.1.1 思想来源

从动物界中的鸟群、兽群和鱼群等的迁移等群体活动而来。在群体活动中，群体中的每一个个体都会受益于所有成员在这个过程中所发现和累积的经验。

1.1.2 基本原理

以鸟群觅食为例，与粒子群优化算法作对比，如上。

在粒子群优化算法中，鸟群中的每个小鸟被称为“粒子”，且同小鸟一样，具有速度和位置。

通过随机产生一定数量的粒子（具体定多少数量后面会讲）作为问题搜索空间的有效解，然后进行迭代搜索，通过该问题对应的适应度函数确定粒子的适应值，得到优化结果。

那具体怎么迭代搜索呢？后面实例会具体讲到。

且这里记得有所谓的“粒子本身的历史最优解”和“群体的全局最优解”，这两个用来影响粒子的速度和下一个位置，借此求得最优解。

1.2.1 基本流程

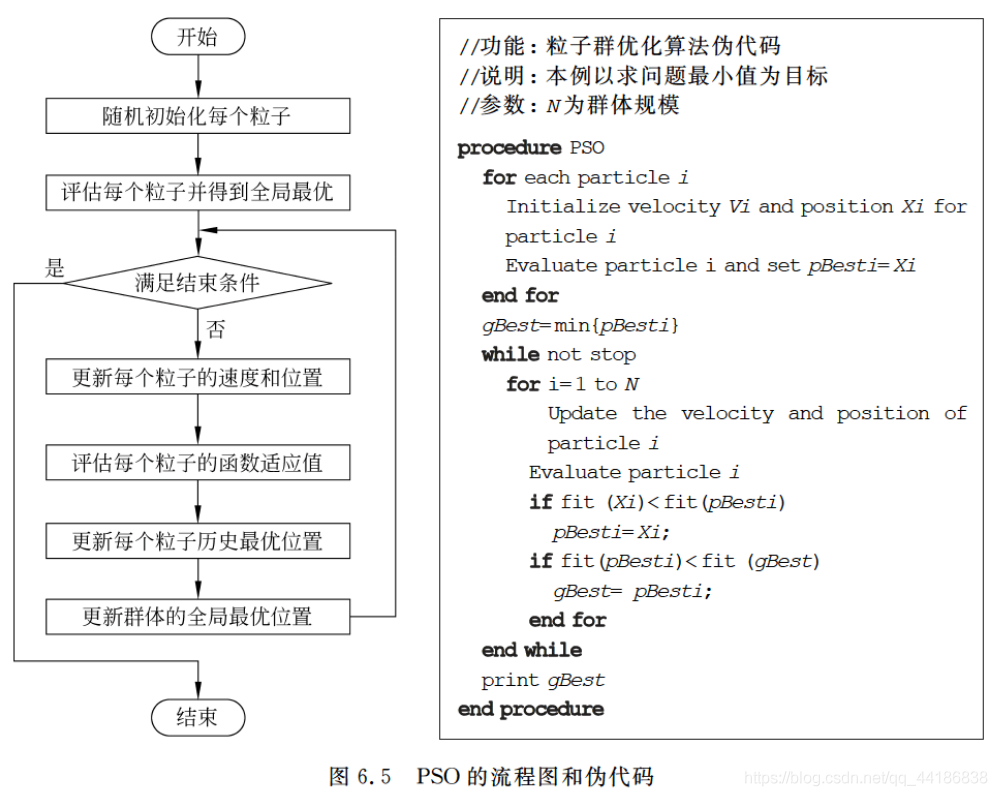
来看一下PSO的算法步骤：
（1）初始化所有粒子，即给它们的速度和位置赋值，并将个体的历史最优pBest设为当前位置，群体中的最优个体作为当前的gBest。
（2）在每一代的进化中，计算各个粒子的适应度函数值。
（3）如果当前适应度函数值优于历史最优值，则更新pBest。
（4）如果当前适应度函数值优于全局历史最优值，则更新gBest。
（5）对每个粒子i的第d维的速度和位置分别按照公式6.1和公式6.2进行更新：

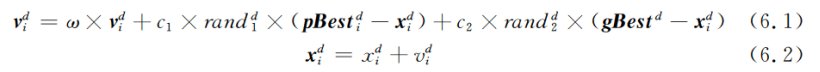
（6）判断是否达到了结束条件（具体怎么定义后面会提），否的话就转到（2）继续执行。

算法流程图和伪代码

1.2.2 应用举例

上面看不懂？

没关系，看了这个实例，保证你能理解最简单的PSO是如何实现的。

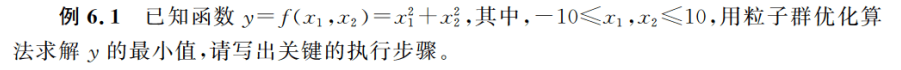
注意对于越界的位置，需要进行合法性调整，将超出定义范围的数值改成范围内的边界值。

1.3 粒子群优化算法的改进研究

粒子群优化算法的研究内容和改进方向

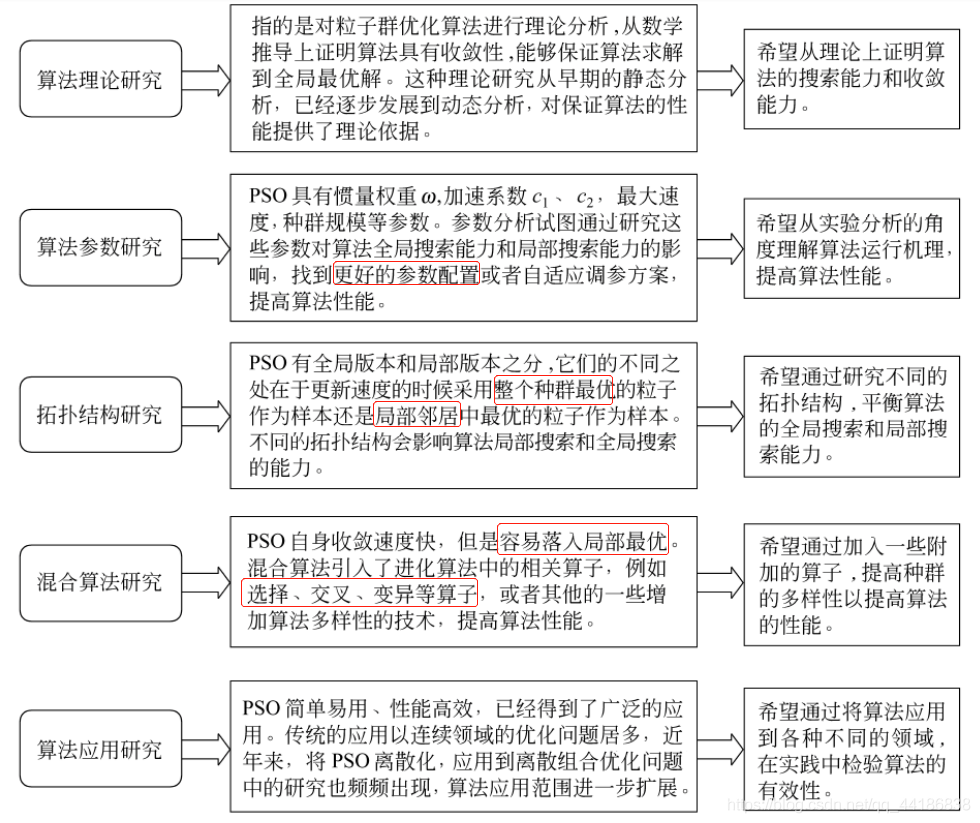
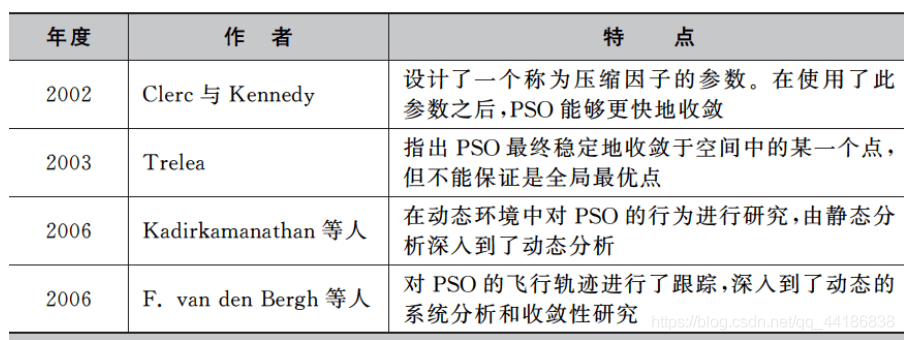
1.3.1 理论研究改进

年代久远，看看就成了。

1.3.2 拓扑结构改进

1.静态拓扑结构‘’

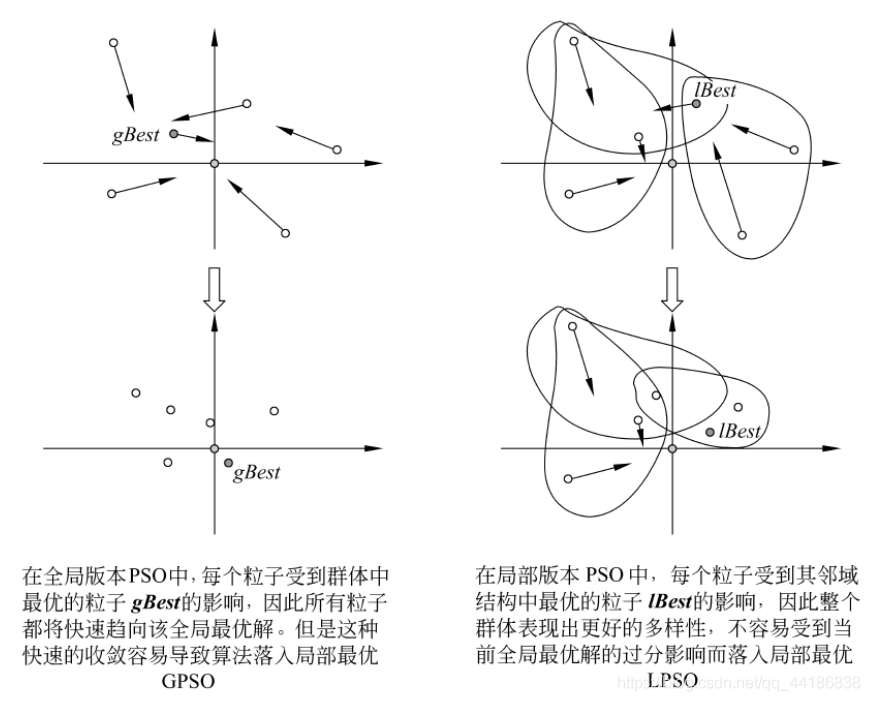
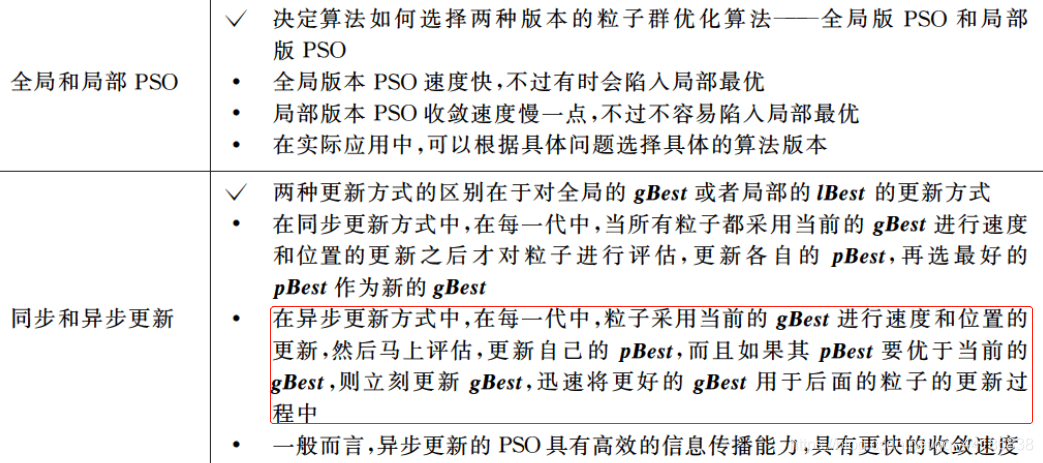
全局版本（Global Version PSO, GPSO）和局部版本（Local Version PSO, LPSO）两个主要范式。

两者主要区别在于社会网络结构的定义不同。

从全局和局部其实也不难看出，粒子在更新速度和位置的时候，前者使用到的是自身的历史最好位置pBest和整个群体中最好的位置gBest，而后者的话，每个粒子所处的“社会”不是整体，而是一个小的邻域。更新速度和位置时用到的除了自身最好的历史位置pBest外，还用到邻域中的最好位置lBest作为更新的向导。

不难发现，后者的多样性更好，在处理复杂的问题的时候，LPSO也会表现出更好的性能。

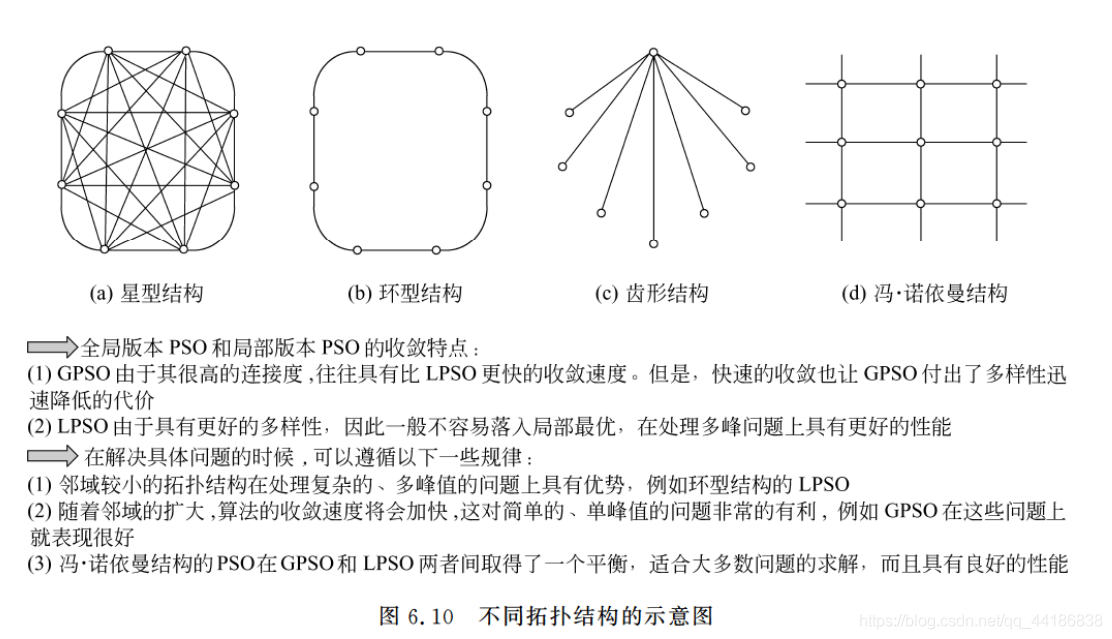
2.动态拓扑结构

由于即使是LPSO也很容易陷入局部最优的问题，而研究动态拓扑结构是希望能够通过在不同的进化阶段使用不同的拓扑结构，动态地改变算法的探索能力和开发能力，在保种群多样性和算法收敛性上取得动态的变化和平衡，以提高算法的整体性能。

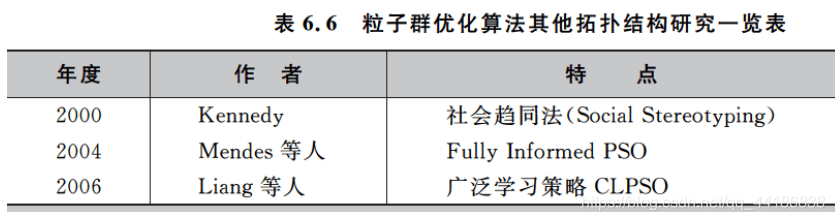
3.其他拓扑结构

1.3.3 混合算法改进

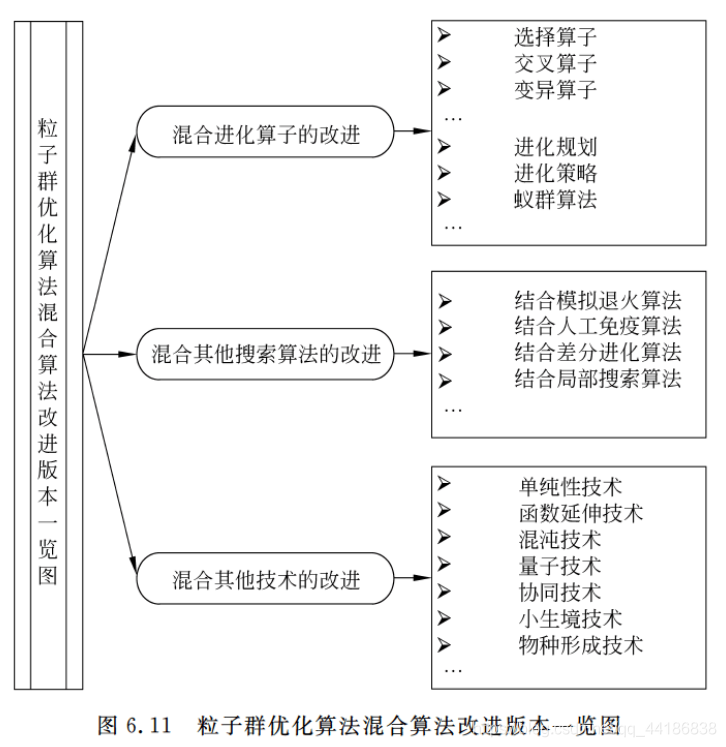
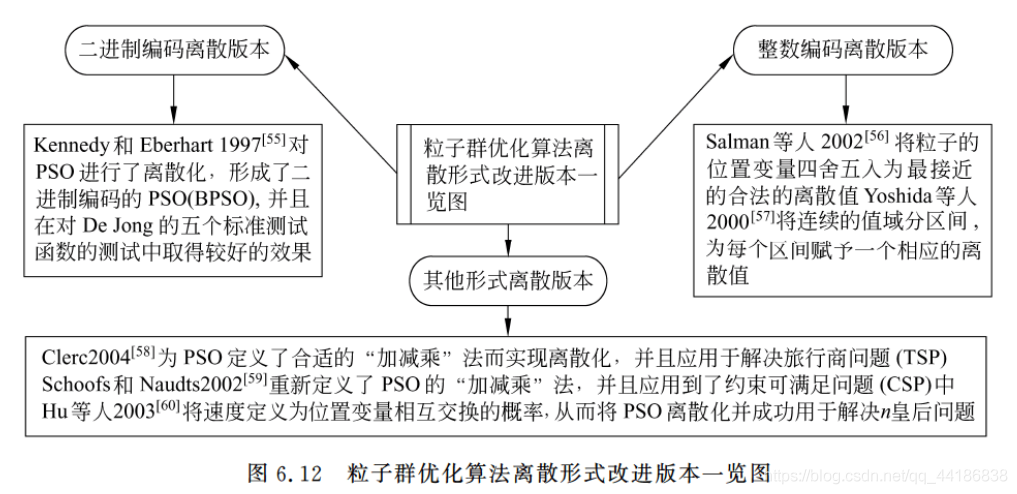
1.3.4 离散版本改进

PSO是非常适合于连续领域问题优化的算法，且已经在此取得相当成功的应用。

离散版本改进将PSO运用到离散领域（组合优化）之中。

在众多的离散PSO改进版本中，二进制编码PSO和整数编码PSO是常见的两种形式。

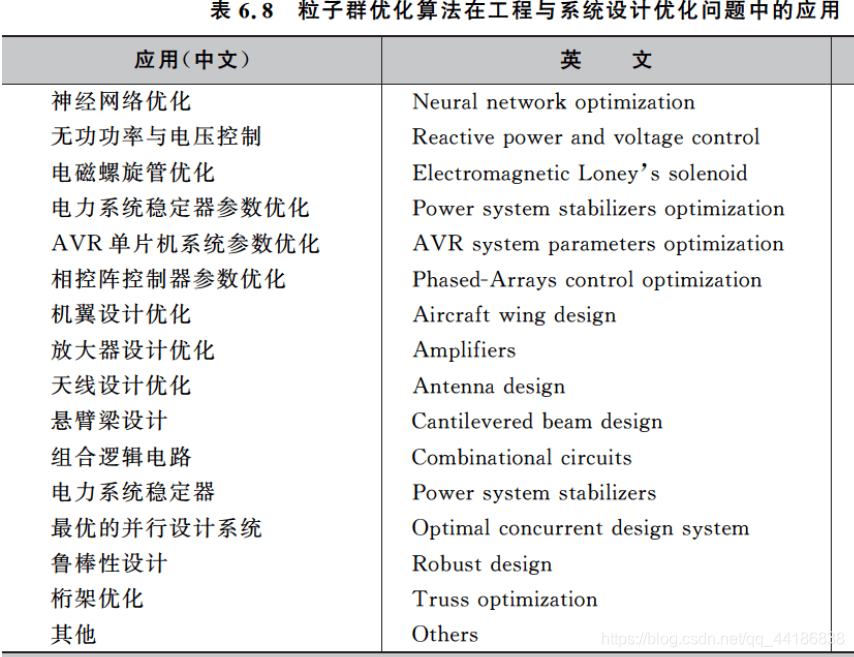
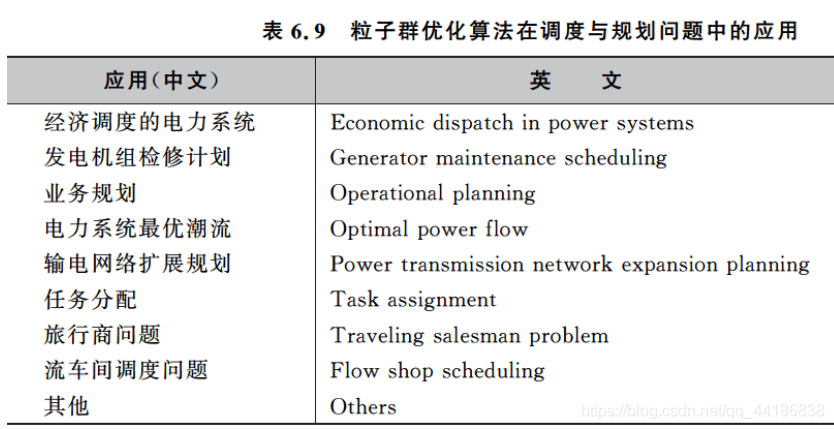
1.4 相关应用

年代久远，看看就成。

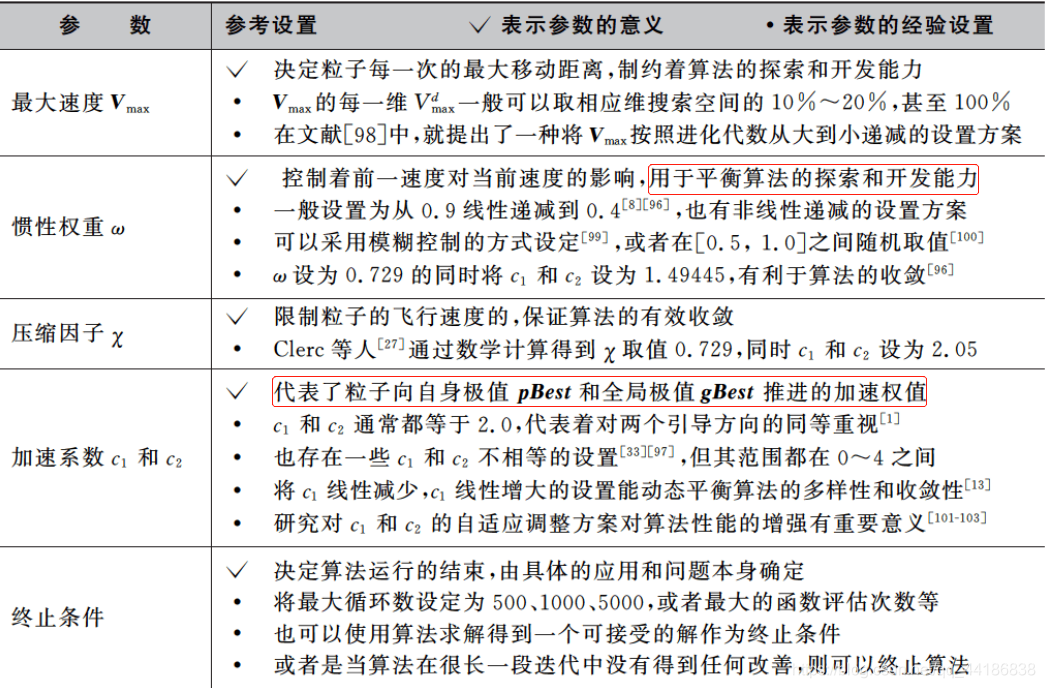
1.5 参数设置

一直在学习路上！

感兴趣的朋友可以点击关注哦！

代码下载链接，有需要的请自行提取，不想hua前的朋友，可私聊同我说，我会回复你，但可能会比较慢。祝好！

粒子群优化算法PSO代码复现-机器学习文档类资源-CSDN文库

智能优化算法大礼包【Python】遗传算法、蚁群优化算法、粒子群算法、禁忌搜索算法-机器学习文档类资源-CSDN