Python每日一谈｜No.35.实例.15.GWO（灰狼优化算法，Grey wolf optimization）

发布日期：2024-04-22 14:02浏览次数：68

欢迎关注我的微信公众号：DrugSci

灰狼优化算法

以前没听过，就拿来试试手

e。。。。话说启发式算法，我觉得我也能搞个Start War算法hhh。

以前，也应该有GA和MC的练习，可以看看其余的算法实现，不过好像意义不是很大。

找时间看看深度学习的基本原理和算法，话说那个比较火。。

优化算法常被用于各个方面，一般来说，优化算法可以被简写为：

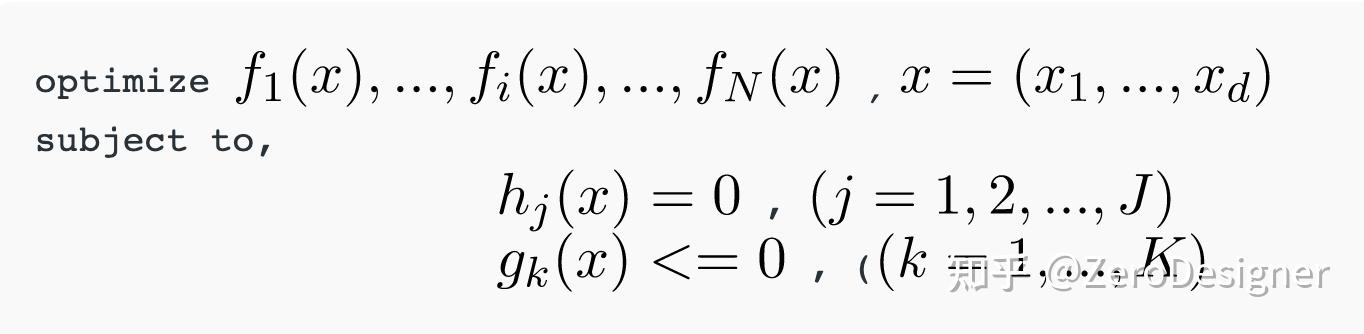
在这里f1, …, fN 为目标（objectives），你也可以认为求解的函数

hj 和 gk 为平等与不平等约束（equality and inequality constraints）

常见的算法有： Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Genetic Algorithms (GA)等等

灰狼优化算法（GWO）是一种基于群体的元启发式算法，模拟自然界中狼群的领导阶层和狩猎机制，由Seyedali Mirjalili等人于2014年提出。

Tips：

灰狼被认为是顶级猎食者，位于食物链的顶端
灰狼常常群居，每个种群平均存在5-12个个体
群体中的所有个体都有非常严格的社会支配等级

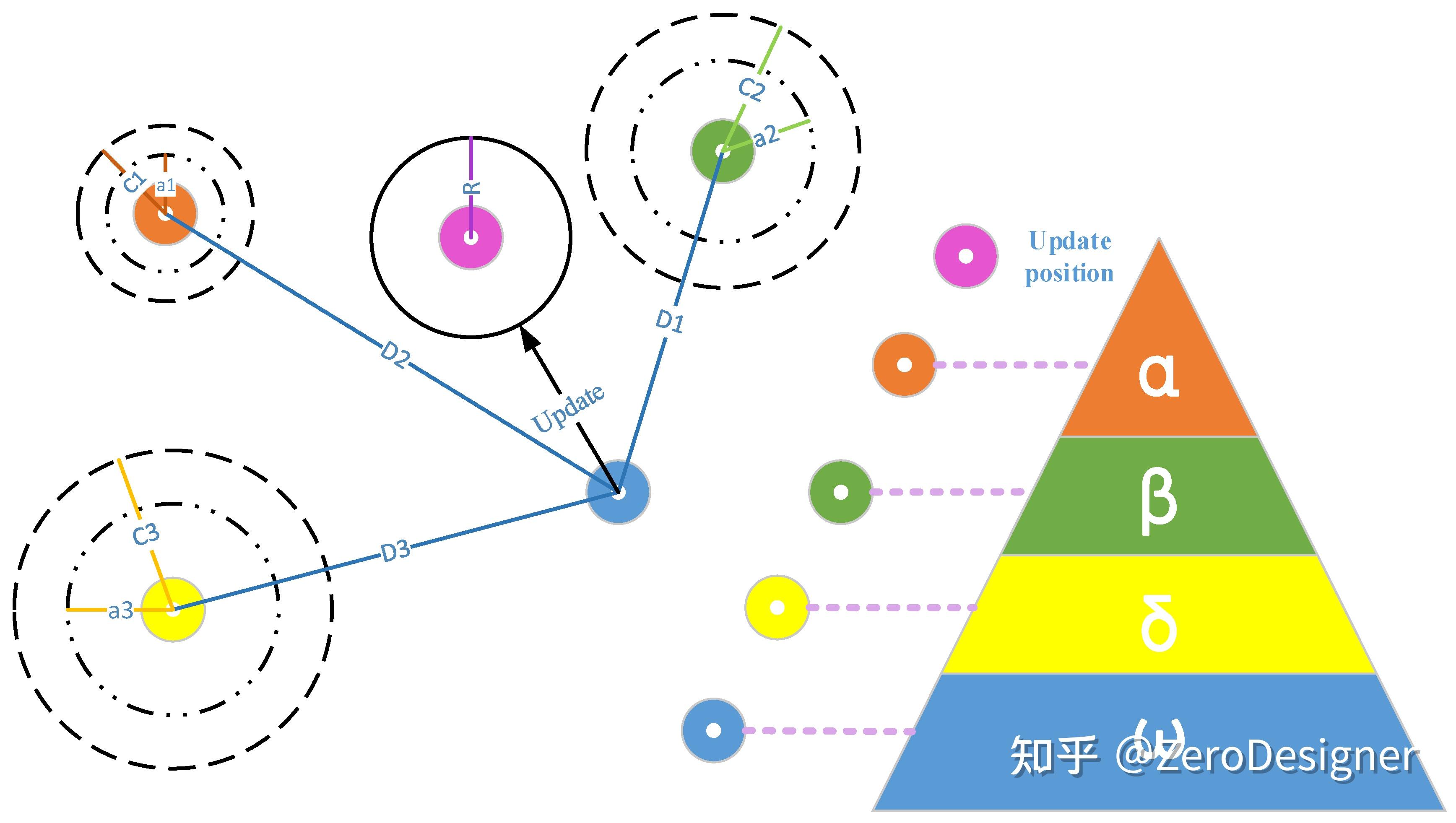
解释：

α狼被认为是狼群中的王，狼群成员应遵守其命令。
β狼是从属狼，帮助α进行决策，被认为是成为α的最佳候选者。
δ狼必须服从α和β，但它们支配着ω。ω有不同的种类的，如侦察兵、哨兵、长老、猎人、看护人等。
ω狼是狼群中最不重要的个体，最后只能吃东西，而不能进行决策。

最优解决方案 Alpha wolf (α)
次优解决方案 Beta wolf (β)
第三优解决方案 Delta wolf (δ)
其余候选解决方案 Omega wolves (ω)

t 代表当前的迭代，$$\\vec{A}$$ ，$$\\vec{C}$$ 代表系数向量，$$\\vec{Xp}$$ 代表猎物的位置向量，$$\\vec{X}$$代表狩猎狼

在迭代过程中， $$\\vec{a}$$ 线性的从2减少为0，$$\\vec{r_1}$$ , $$\\vec{r_2}$$ 则是从[0, 1]中随机选择的向量

在每次迭代过程中，ω狼会根据α, β, δ狼来更新其位置，因为α, β, δ狼要更加清楚猎物的潜在位置

当猎物停止移动时，灰狼会停止狩猎过程，然后袭击猎物

我们减少$$\\vec{a}\\cdot \\vec{A}$$ 的值，这个值子迭代过程值一直位于$$[-2a, 2a]$$,$$a$$会在迭代过程中从2减少到0

$$|A|<1$$ 会强迫狼群袭击猎物

$$|A|>1$$ 强迫狩猎狼群离开猎物，并寻找一个更合适的猎物

GWO中另一个支持探索的组件是$$C$$。它是$$[0，2]$$之间的随机值。$$C> 1$$重视攻击，而$$C<1$$则不重视攻击。

Step1: 随机起始灰狼种群中的个体数$$ Xi(i=1,2,…,n)$$
Step2: 赋予a的初始值为2，赋予A以及C值，根据等式3
Step3：

计算种群中每个个体的适应度

$$Xα$$=拥有最优值的个体
$$Xβ$$=拥有第二优值的个体
$$Xδ$$=拥有第三优值的个体
Step4:

对于 t=1 直到最大迭代数(t=max):

更新ω狼的位置，依据等式4, 5 and 6
更新 a, A, C，依据等式3
$$a=2(1-t/T)$$
计算所有个体的适应度
更新 $$Xα, Xβ, Xδ$$.
? 结束循环
Step5: 返回$$ Xα$$

$$Z=np.sin(X 2) + np.cos(Y2)$$

范围： $$X[-3,3]，Y[-3,3]$$

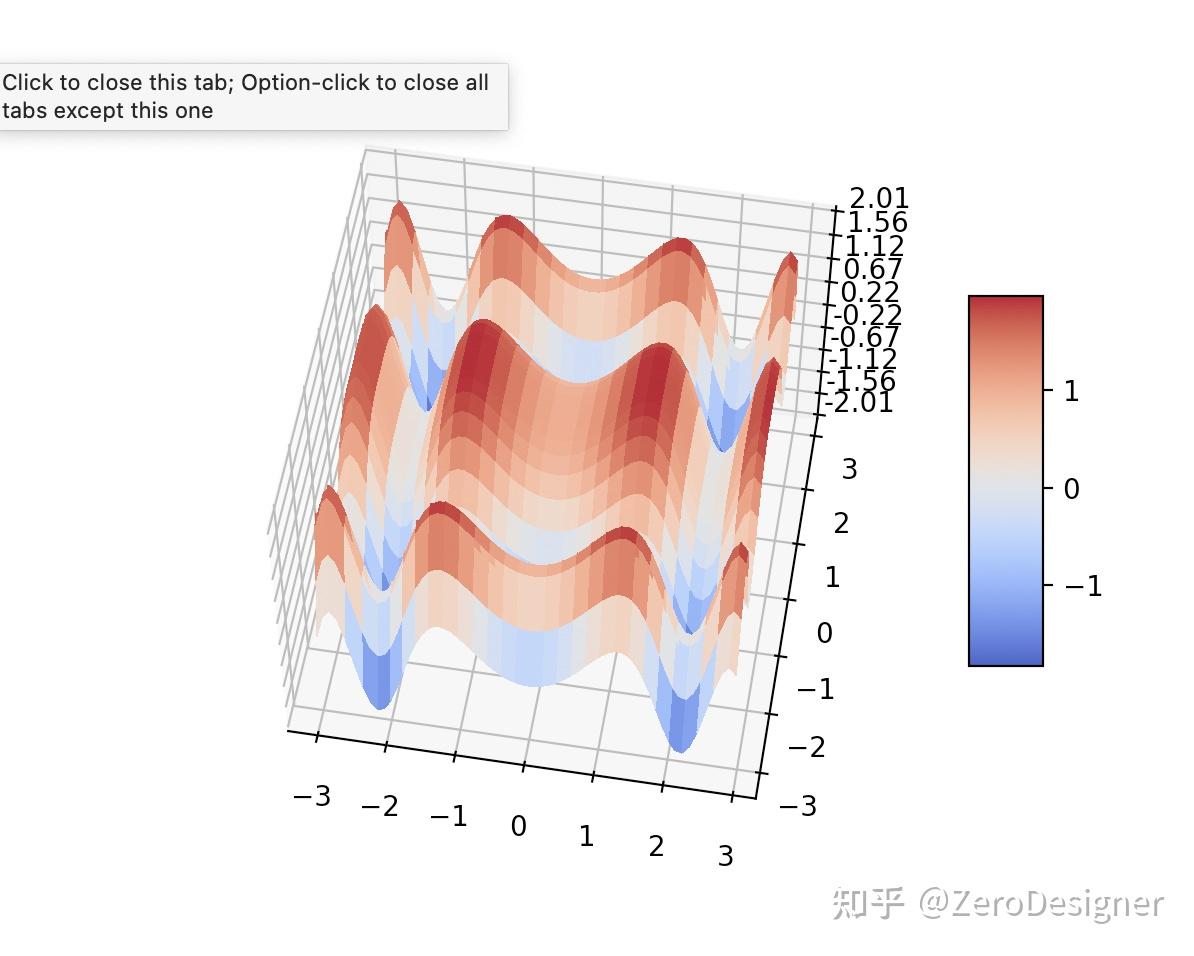
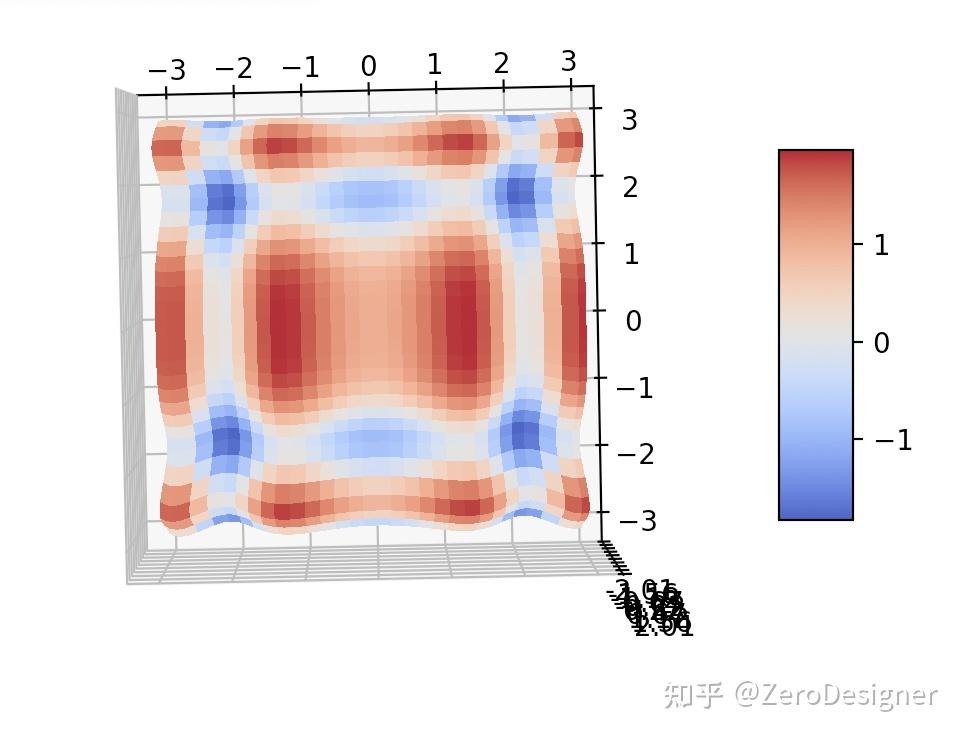
import  numpy as np
import random
import copy

def get_fitness(ori_w_p):
    # 设置适应度函数
#    return np.absolute(np.sin(ori_w_p[0])*np.cos(ori_w_p[1]) + np.sin((ori_w_p[0]-10)/10)*2 + np.sin((ori_w_p[1]-10)/10))*2
    return np.sin(ori_w_p[0] **2) + np.cos(ori_w_p[1]**2)

def initial_group(num):
    # 随机起始灰狼种群，根据输入的num进行设置，并输出其（x,y,z）值
    wolves_dict = {}
    ori_w_range_x = np.arange(-3, 3, 0.1)
    ori_w_range_y = np.arange(-3, 3,0.1)
    for i in range(num):
        ori_w_p_x = random.choice(ori_w_range_x)
        ori_w_p_y = random.choice(ori_w_range_y)
        ori_w_p = [ori_w_p_x,ori_w_p_x]
        #wolves_dict['wolf_'+str(i)]=[ori_w_p[0],ori_w_p[1], get_fitness(ori_w_p)]
        wolves_dict[i] = {'x':ori_w_p_x,'y':ori_w_p_y,'z':get_fitness(ori_w_p)}

    return wolves_dict

import pandas as pd

def sort_wolves(wolves_dict):
    # 将灰狼种群分类，分为a,b,c,d四个等级
    wolves = pd.DataFrame(wolves_dict)
    wolves = wolves.T
#    wolves.columns=['x','y','z']
    wolves.sort_values(by='z', ascending=False, inplace =True)
    wolves.reset_index(drop=True, inplace=True)
    wolves_level = []
    wolves_level.extend(list('a'))
    wolves_level.extend(list('b'*3))
    wolves_level.extend(list('c'*9))
    wolves_level.extend(list('d'*20))
    wolves_id = [ 'wolf_'+str(i) for i in range(len(wolves_level))]
    wolves['level'] = wolves_level
    wolves['id'] = wolves_id
    wolves_T = wolves.T
    return wolves_T.to_dict()


def get_iteration_param(t_n,total_nums):
    v_r1 = random.random()
    v_r2 = random.random()
    v_c = 2 * v_r2
    prey_range_x = np.arange(-30, 15, 0.1)
    prey_range_y = np.arange(-30, 15, 0.1)
    v_xp = np.array([random.choice(prey_range_x),random.choice(prey_range_y)])
    v_D = np.absolute(v_c * v_xp - v_xp)
    v_a = 2 - t_n/total_nums * 2
    v_A = 2 * v_a * v_r1 - v_a
    return v_A,v_D

def get_iteration_param_2(t_n,total_nums,wolve_a):
    # 拿到迭代参数
    v_r1 = random.random()
    v_r2 = random.random()
    v_c = 2 * v_r2
    v_xp = np.array([wolve_a['x'],wolve_a['y']])
    v_D = np.absolute(v_c * v_xp - v_xp)
    v_a = 2 - t_n/total_nums * 2
    v_A = 2 * v_a * v_r1 - v_a
    return v_A,v_D

def omega_find_leader(wolves_group):
    # 发现omega狼周围的领导者
    # 离其最近的三匹高级狼
    # a等级一匹
    # b等级一匹，距离最短的
    # c等级一匹，距离最短的
    a_w = []
    b_w = []
    c_w = []
    d_w = []

    for i in wolves_group.keys():
        if wolves_group[i]['level'] == 'a':
            a_w.append(wolves_group[i])
        elif wolves_group[i]['level'] == 'b':
            b_w.append(wolves_group[i])
        elif wolves_group[i]['level'] == 'c':
            c_w.append(wolves_group[i])
        elif wolves_group[i]['level'] == 'd':
            d_w.append(wolves_group[i])

    for i in d_w:
        i['leader_group'] = [a_w[0]['id']]
        i['leader_group'].append(find_shortest_leader(i,b_w)['id'])
        i['leader_group'].append(find_shortest_leader(i,c_w)['id'])
    return d_w


def find_shortest_leader(worker,leaders):
    leader_id = []
    leader_dist = []
    for l in leaders:
        dist = np.linalg.norm(np.array([l['x'],l['y']])- np.array([worker['x'],worker['y']]))
        #dist=np.sqrt(sum(np.power((np.array(l['x'],l['y'])- np.array(worker['x'],worker['y'])), 2)))
        leader_id.append(l)
        leader_dist.append(dist)
    return leader_id[leader_dist.index(min(leader_dist))]


def iteration(wolves_group,t_n,total_nums,wolve_a):
    # 根据文本中的公式进行迭代
    wolves_group_cg = wolves_group
    for i in wolves_group_cg:
        ind = wolves_group_cg[i]
        if ind['level'] == 'a':
            x_p = np.array([ind['x'],ind['y']])
            v_A,v_D = get_iteration_param_2(t_n,total_nums,wolve_a)
            v_x = x_p - (v_A * v_D)
            ind['x'] = v_x[0]
            ind['y'] = v_x[1]
            ind['z'] = get_fitness([v_x[0],v_x[1]])
        elif ind['level'] == 'b':
            x_p = np.array([ind['x'],ind['y']])
            v_A,v_D = get_iteration_param_2(t_n,total_nums,wolve_a)
            v_x = x_p - (v_A * v_D)
            ind['x'] = v_x[0]
            ind['y'] = v_x[1]
            ind['z'] = get_fitness([v_x[0],v_x[1]])
        elif ind['level'] == 'c':
            x_p = np.array([ind['x'],ind['y']])
            v_A,v_D = get_iteration_param_2(t_n,total_nums,wolve_a)
            v_x = x_p - v_A * v_D
            ind['x'] = v_x[0]
            ind['y'] = v_x[1]
            ind['z'] = get_fitness([v_x[0],v_x[1]])
        elif ind['level'] == 'd':
            del ind

    wolves_group_cg_t = copy.deepcopy(wolves_group_cg)
    count = len(wolves_group_cg_t)
    #print(count)
    wolves_list = [i for i in wolves_group_cg_t]
    for i in wolves_list:
        if wolves_group_cg_t[i]['level'] == 'd':
            del wolves_group_cg_t[i]

    count = len(wolves_group_cg_t)
    #print(count)

    omega_leaders = omega_find_leader(wolves_group)
    omega_leaders_cg = get_omega_next(omega_leaders,wolves_group_cg_t)
#    print('omega_leaders_cg',omega_leaders_cg)
    for i in range(len(omega_leaders_cg)):
        wolves_group_cg_t[ i + count + 1] = omega_leaders_cg[i]

    return wolves_group_cg_t

def get_omega_next(omega_leaders,wolves_group_cg):
    # 拿到omega狼的下一步位置
    for i in omega_leaders:
        leader_group = [[x,wolves_group_cg[x]] for x in wolves_group_cg if wolves_group_cg[x]['id'] in i['leader_group']]
        i['x'] = (leader_group[0][1]['x']+leader_group[1][1]['x']+leader_group[2][1]['x'])/3 
        i['y'] = (leader_group[0][1]['y']+leader_group[1][1]['y']+leader_group[2][1]['y'])/3 
        del i['leader_group']
    return omega_leaders


if __name__ == '__main__':
    # 进入主函数阶段
    # 起始生成种群数33匹狼
    # a等级：1
    # b等级：3
    # c等级：9
    # d等级：21
    import time
    a = time.time()
    fit_list = []
    initial_wolves = initial_group(33)
    wolves_sort = sort_wolves(initial_wolves)
    wolves_group_cg = iteration(wolves_sort,1,100,wolves_sort[0])
    for x in wolves_group_cg:
        fit_list.append(wolves_group_cg[x]['z'])
    # 查看第一代狼群中的最优值
    print('round ',str(1),max(fit_list))
    print('########################')

    # 设置一个狼群记忆库，记录迭代拿到的最大值
    wolves_memory = [max(fit_list)]

    # 进行迭代
    count = 0
    # 设置记数器
    for i in range(100):
    # 迭代100次
        wolves_sort = sort_wolves(wolves_group_cg)
        wolves_group_cg = iteration(wolves_group_cg,i+2,100,wolves_group_cg[0])
        fit_list = []
        for x in wolves_group_cg:
            fit_list.append(wolves_group_cg[x]['z'])
        # 如果生成了比记忆库还好的值，植入记忆库中
        if max(fit_list) > max(wolves_memory):
            print('wolves get better')
            wolves_memory.append(max(fit_list))
        # 如果生成了比记忆库最小值还坏的值，记数器加1
        elif max(fit_list) <= min(wolves_memory):
            count = count + 1
            print('wolves get bad')
        print('round ',str(i + 2),max(fit_list))
        print('wolves memory ',max(wolves_memory))
        print('########################')
        # 如果记数器达到20，停止
        if count == 20:
            b = time.time()
            print('$$$$$$$$$$$$$$$$$$$$$$')
            print('Touch The top')
            print('Cost:',b-a)
            break

round  1 1.7867094985136402
wolves get better
########################
round  2 1.88412723934572
wolves memory  1.88412723934572
########################
wolves get bad
round  3 1.7209958013554358
wolves memory  1.88412723934572
########################
wolves get bad
round  4 1.690852124797344
wolves memory  1.88412723934572
########################
wolves get bad
round  5 1.5915389773852602
wolves memory  1.88412723934572
########################
wolves get bad
round  6 1.085831282210004
wolves memory  1.88412723934572
########################
wolves get bad
round  7 1.2958203101169712
wolves memory  1.88412723934572
########################
wolves get better
round  8 1.9451995063321545
wolves memory  1.9451995063321545
########################
wolves get bad
round  9 1.7659827231658738
wolves memory  1.9451995063321545
########################
wolves get bad
round  10 1.6735075166421174
wolves memory  1.9451995063321545
########################
wolves get bad
round  11 1.085831282210004
wolves memory  1.9451995063321545
########################
wolves get bad
round  12 1.2882804684159321
wolves memory  1.9451995063321545
########################
wolves get bad
round  13 1.3365358275832184
wolves memory  1.9451995063321545
########################
wolves get bad
round  14 1.7148546855825482
wolves memory  1.9451995063321545
########################
wolves get bad
round  15 1.6493457575609682
wolves memory  1.9451995063321545
########################
wolves get bad
round  16 1.6495890340795554
wolves memory  1.9451995063321545
########################
wolves get bad
round  17 1.5746177374545502
wolves memory  1.9451995063321545
########################
round  18 1.90873868646127
wolves memory  1.9451995063321545
########################
wolves get bad
round  19 1.5595696014192248
wolves memory  1.9451995063321545
########################
wolves get bad
round  20 1.669455744321212
wolves memory  1.9451995063321545
########################
wolves get better
round  21 1.998311251689651
wolves memory  1.998311251689651
########################
wolves get bad
round  22 1.724201338492482
wolves memory  1.998311251689651
########################
round  23 1.994730665848572
wolves memory  1.998311251689651
########################
wolves get bad
round  24 1.2921623982236445
wolves memory  1.998311251689651
########################
round  25 1.9276920925952434
wolves memory  1.998311251689651
########################
round  26 1.9388407753727679
wolves memory  1.998311251689651
########################
wolves get bad
round  27 1.455602314998224
wolves memory  1.998311251689651
########################
round  28 1.9754371016267238
wolves memory  1.998311251689651
########################
round  29 1.981699645380968
wolves memory  1.998311251689651
########################
round  30 1.9947710900851012
wolves memory  1.998311251689651
########################
round  31 1.996871277566931
wolves memory  1.998311251689651
########################
round  32 1.9904021425055562
wolves memory  1.998311251689651
########################
round  33 1.9841458250922928
wolves memory  1.998311251689651
########################
round  34 1.9798460151563981
wolves memory  1.998311251689651
########################
round  35 1.9617377164271952
wolves memory  1.998311251689651
########################
round  36 1.976503078025663
wolves memory  1.998311251689651
########################
round  37 1.9677819094389473
wolves memory  1.998311251689651
########################
round  38 1.942933712239012
wolves memory  1.998311251689651
########################
round  39 1.9693344001603683
wolves memory  1.998311251689651
########################
round  40 1.9523287238135731
wolves memory  1.998311251689651
########################
round  41 1.980265330731481
wolves memory  1.998311251689651
########################
wolves get better
round  42 1.9989088559712567
wolves memory  1.9989088559712567
########################
round  43 1.9974455082492018
wolves memory  1.9989088559712567
########################
round  44 1.9932304547448385
wolves memory  1.9989088559712567
########################
wolves get bad
round  45 1.6697485606968883
wolves memory  1.9989088559712567
########################
$$$$$$$$$$$$$$$$$$$$$$
Touch The Top
Cost: 0.5387866497039795

上一篇：工艺优化,process optimization英语短句,例句大全

下一篇：初中生申请出国留学的途径【优秀5篇】

新宝GG新闻

Python每日一谈｜No.35.实例.15.GWO（灰狼优化算法，Grey wolf optimization）

案例推荐

关于新宝GG

新宝GG注册

新宝GG新闻

新宝GG登录

新宝GG平台

新宝GG代理加盟

联系我们

020-88888888